Introduction to Stopping Conditions

Part B: Stopping Conditions

Introduction

In the preceding section, we introduced an algorithm designed to construct a decision tree. This algorithm incorporates a specific feature known as a stopping condition.

 Question:

Question: If we don’t terminate the decision tree algorithm manually, what will the leaf nodes of the decision tree look like?

Show Answer

Answer: The tree will continue to grow until each leaf node contains exactly one training point and the model attains 100% training accuracy. As you might remember from our previous course, 100% accuracy is a bad thing! It almost certainly means that we have overfit our data.

 Question:

Question: How can we prevent this from happening?

Show Answer

Answer: Stop the tree from growing.

Common Stopping Conditions

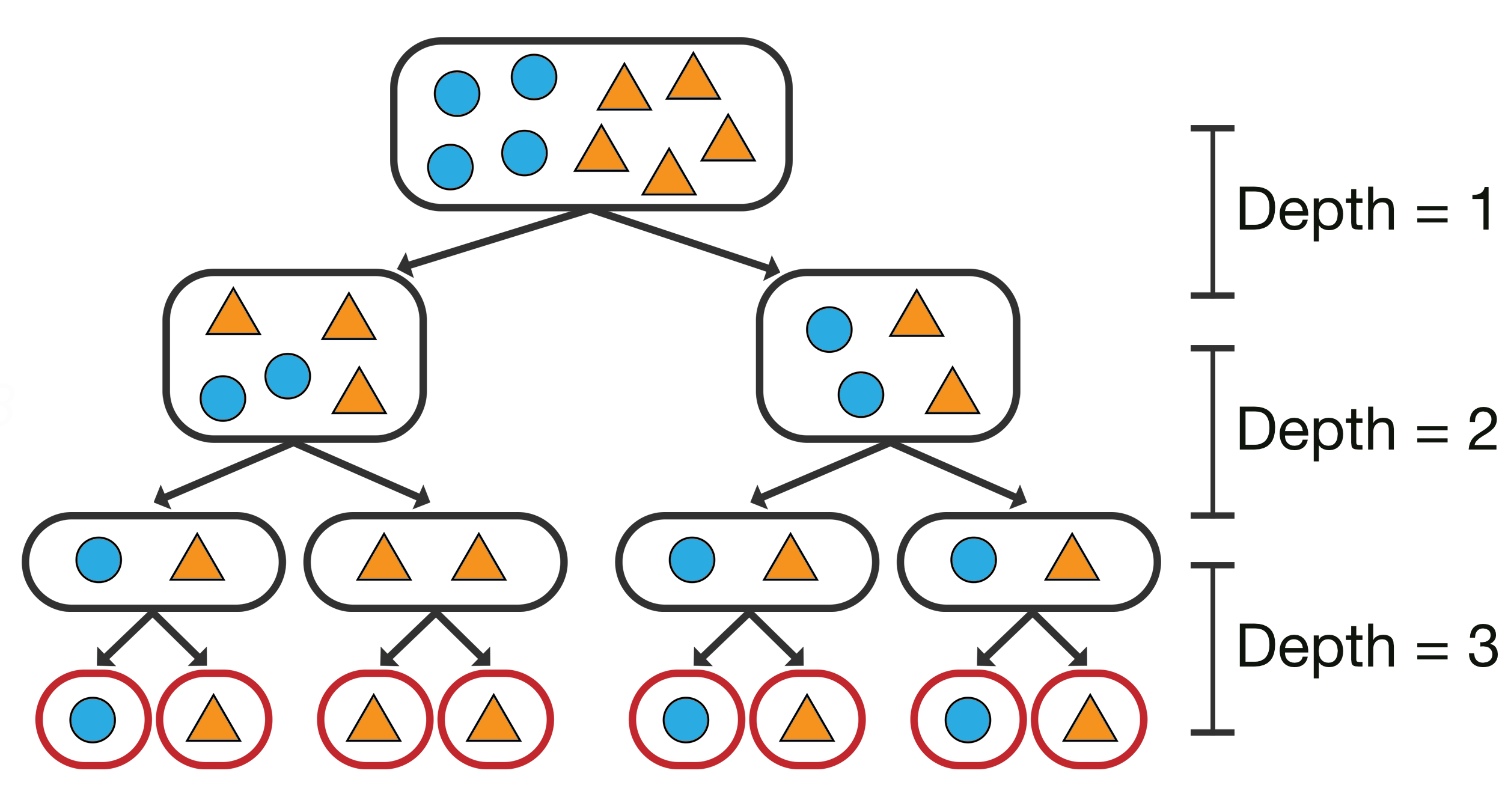
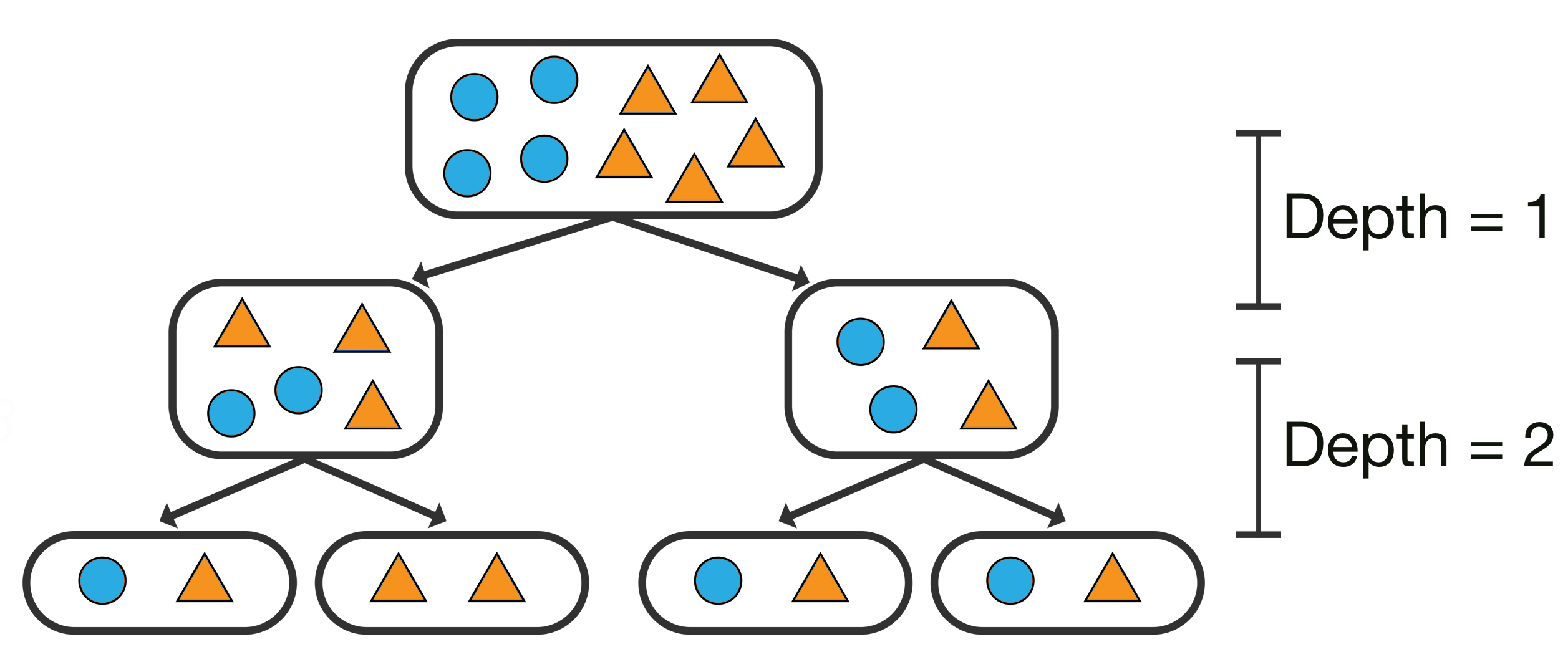
The most common stopping criterion involves restricting the maximum depth (max_depth) of the tree.

The following diagram illustrates a decision tree trained on the same dataset as the previous one. However, a max_depth of 2 is employed to mitigate overfitting.

Four other common simple stopping conditions are:

1. Do not split a region if all instances in the region belong to the same class.
2. Do not split a region if it would cause the number of instances in any sub-region to go below a pre-defined threshold (min_samples_leaf).
3. Do not split a region if it would cause the total number of leaves in the tree to exceed a pre-defined threshold (max_leaf_nodes).
4. Do not split if the gain is less than some pre-defined threshold (min_impurity_decrease).

Let's look at each one individually.

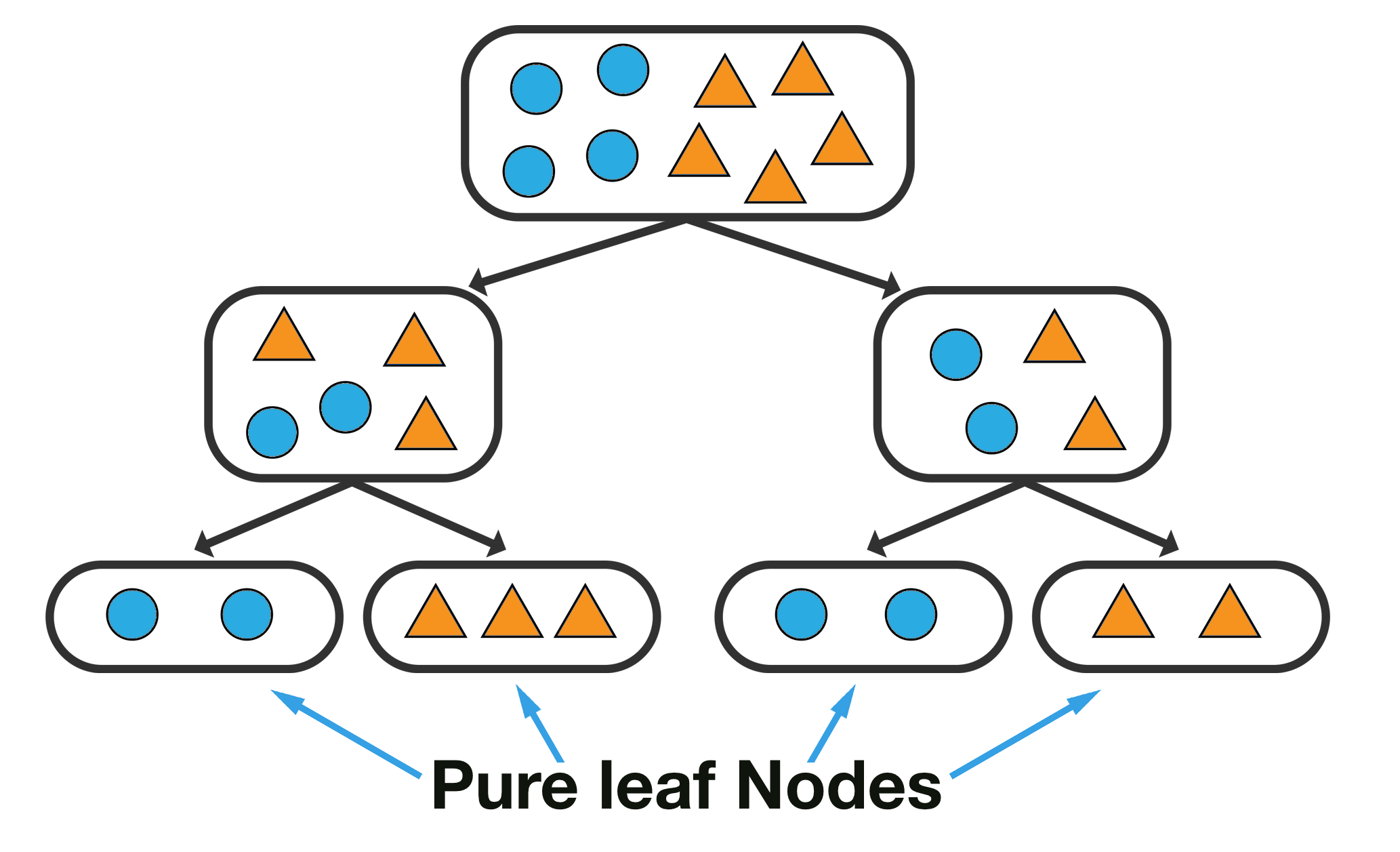
1. Do not split a region if all instances in the region belong to the same class.

The diagram below displays a tree where each of the end leaf nodes are clearly of the same class, therefore we can stop at this point in growing the tree further.

2. Do not split a region if it would cause the number of instances in any sub-region to go below a pre-defined threshold (min_samples_leaf).

In the following diagram, we set min_samples_leaf to be 4, and we can observe that we can't split the tree further because each leaf node already meets the minimum requirement.

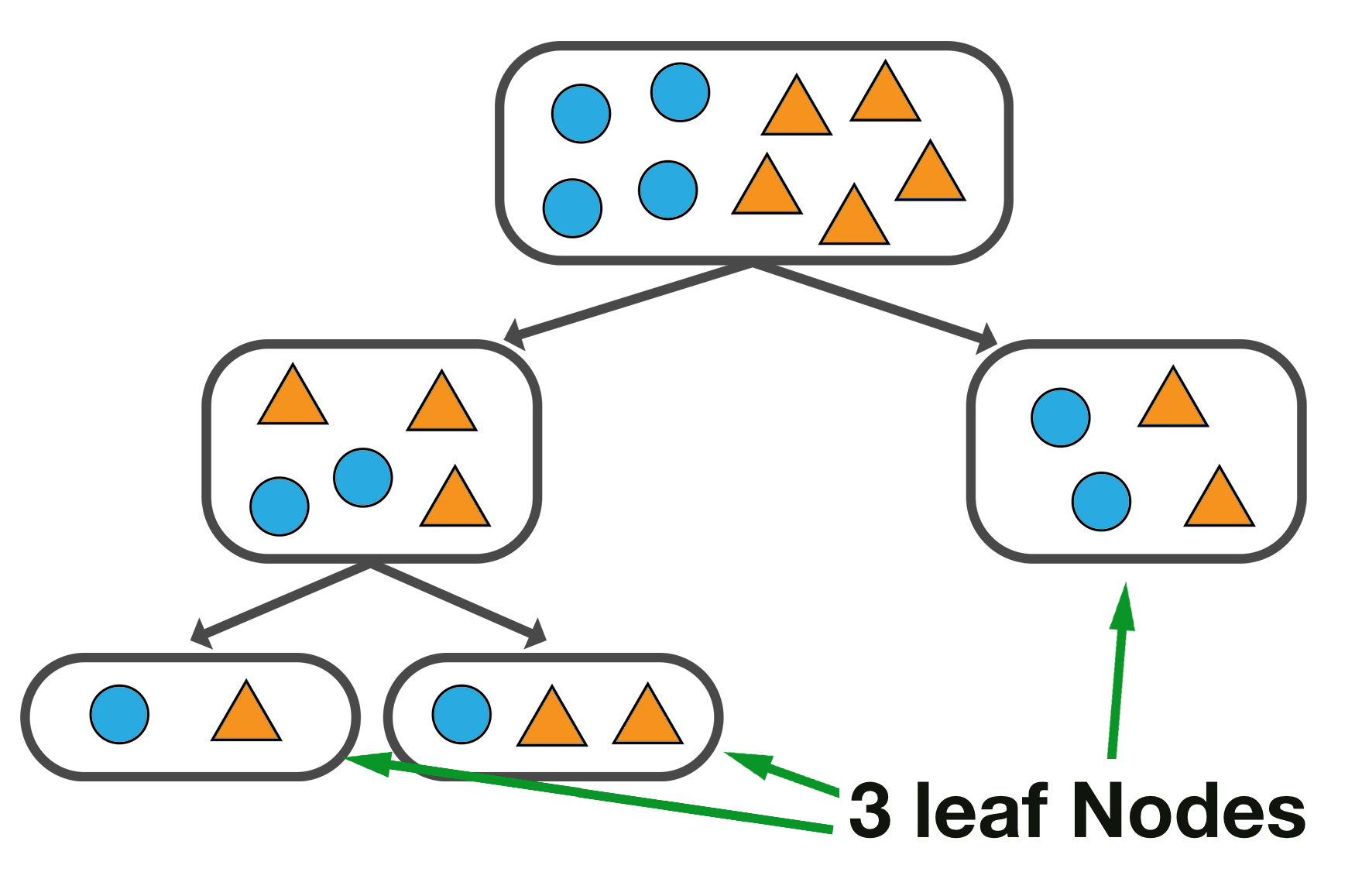
3. Do not split a region if it would cause the total number of leaves in the tree to exceed a pre-defined threshold (max_leaf_nodes).

In the diagram below, we observe a tree with a total of 3 leaf nodes, as specified as the maximum.  

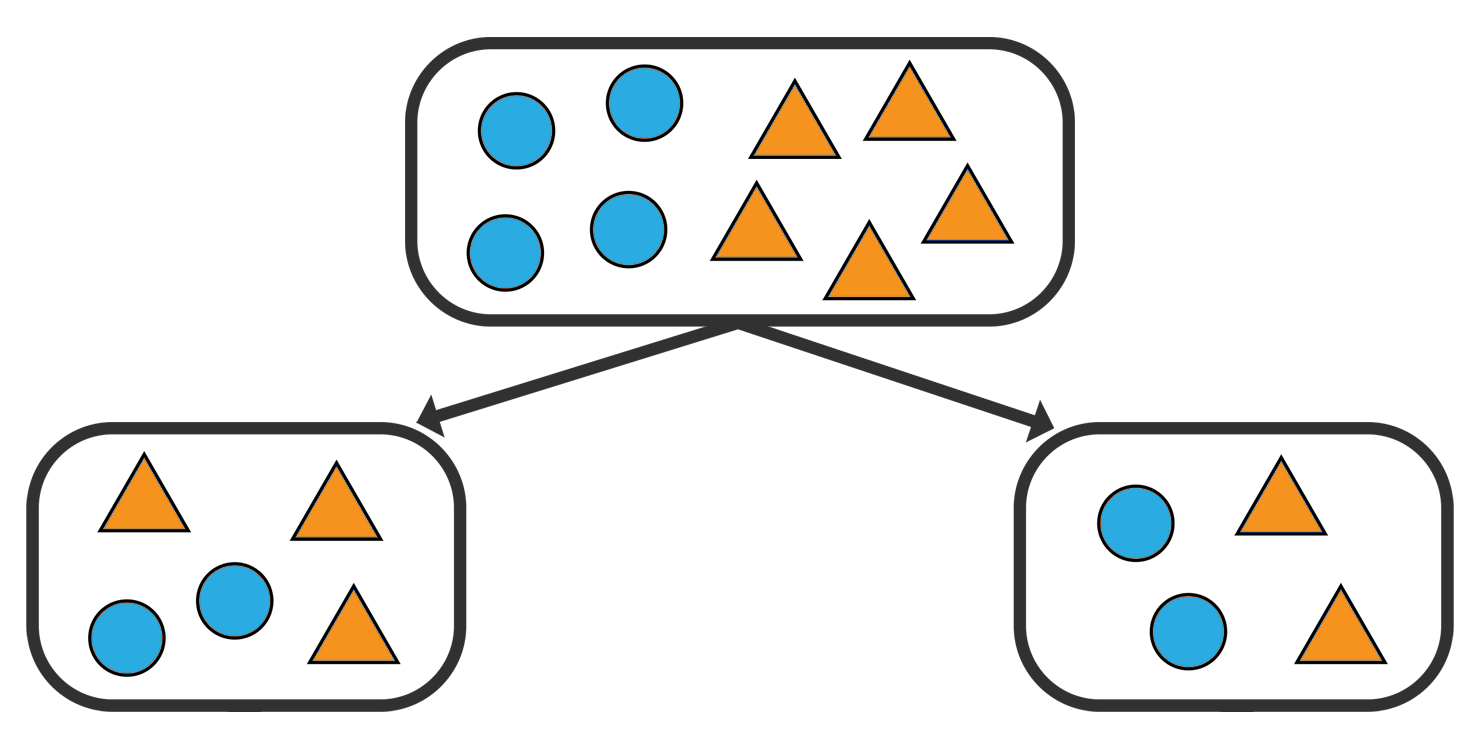
4. Do not split if the gain is less than some pre-defined threshold (min_impurity_decrease).

Compute the gain in purity of splitting a region R into R1 and R2 : 

Note:

M is the classification error, Gini index, or Entropy, depending on which one we have chosen to use.

Scikit-learn (sklearn) grows trees in depth-first fashion by defaul, but when max_leaf_nodes is specified it is grown in a best-first fashion.